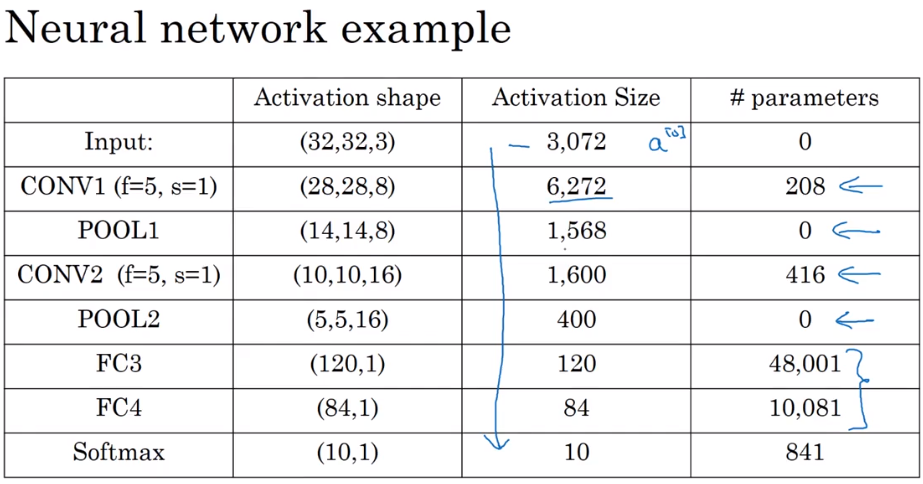
监督学习
由带标签的数据集∑(x_i,y)进行模型训练
线性回归
假设函数: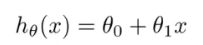
代价函数(损失函数):
线性回归问题即求解代价函数的最小值
梯度下降法
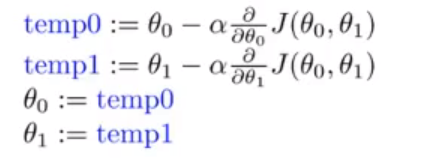
α为步长,控制更新速率,参数同时更新
确定步长:网格搜索或梯度限制
Batch梯度下降
批量梯度下降
每一步更新都遍历整个·训练集,与随机梯度下降相对应
多元梯度下降法
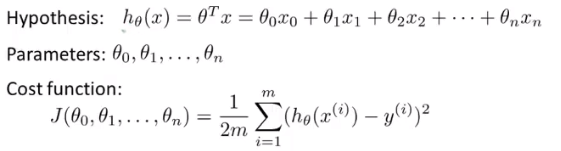

x0=1,两边公式本质相同
特征缩放
将所有特征的取值范围缩放至[-1,1]范围中(通常),加速找到偏导数为0点的进程
均值归一化:用xi-μi代替xi使均值为0
多项式回归
用单一变量的不同次方作为不同的特征值(仅适用于线性回归)
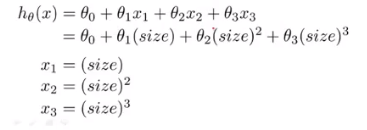
正规方程
参数少时(n<10000)适用,不需要迭代计算

X第一列始终置1
设计矩阵
正规矩阵方法证明:https://blog.csdn.net/chenlin41204050/article/details/78220280
若X不可逆,可以使用伪逆矩阵代替,一般不可逆的原因为特征变量过多
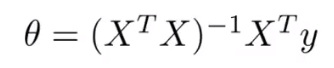
需要考虑XTX是否可逆的问题
线性回归的正则化
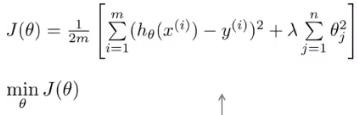
梯度下降
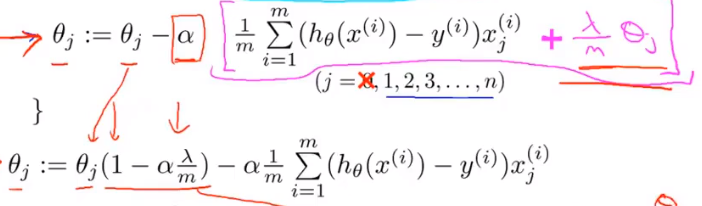
正规方程
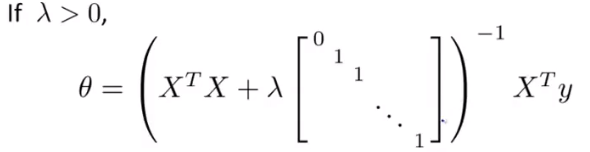
XTX+λ[1]必可逆
逻辑回归
二分类


x与ln(y/1-y)之间具有线性关系,y可视为时间的概率,1-y视为反例得概率。
h_θ(x)表示在给定x和θ情况下预测y=1的概率

决策边界
即θTx所构成的边界,(在二分类中)用于区分h_θ(x)是取1还是0
逻辑回归的代价函数

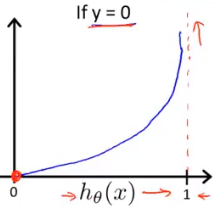
如y=1的cost函数表示,当h(x)->0预测得到y=0的结果时若y=1需要无穷大的代价来修正假设函数;当h(x)->1预测得到y=0的结果时若y=1需要极小的代价来修正假设函数
结论(由最大似然法得到):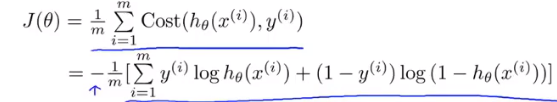
得到代价函数后再使用梯度下降的方法(包括特征缩放等)来推算假设函数
其他可选的回归方法(除了第一条梯度下降,其他方法都具有右边的优点)

多分类问题
一对多思想
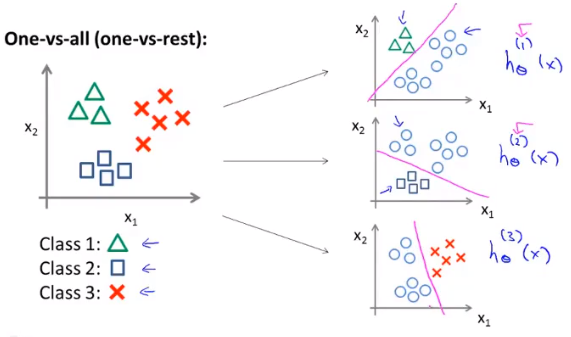
将多分类问题转化为多个二分类问题(分类器)的集合,一一求解
ps:然而多分类问题一般采用深度学习方法解决
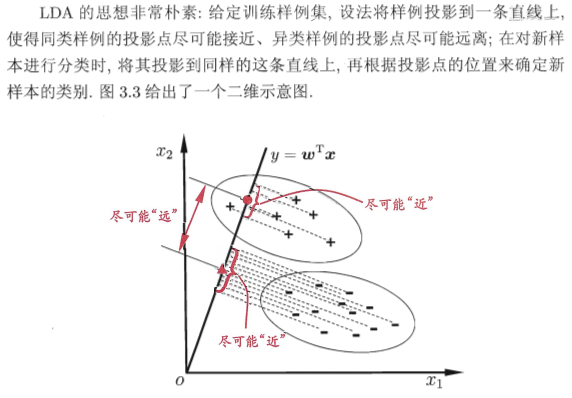
线性判别分析(LDA)
减少过拟合的方法
1.减少特征数量
2.正则化
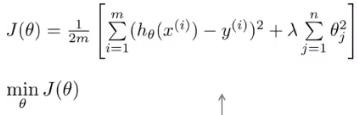
右边整项为正则化项,λ为正则化参数
第一项越低表示拟合程度越高;第二项越低,参数越小,模型越简单,避免过拟合的可能越高
若λ过大,可能会将所有参数全都消去,转变成欠拟合
逻辑回归的正则化
添加后一项以减少变量数量

非线性假设
神经网络
MP模型
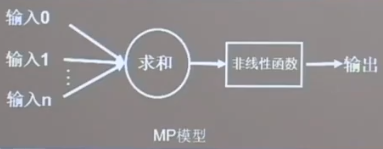
每一层添加偏置项x0
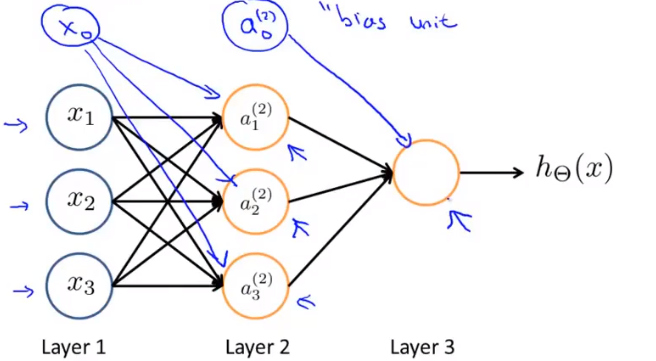
第一层为输入层,第二层之上为隐藏层
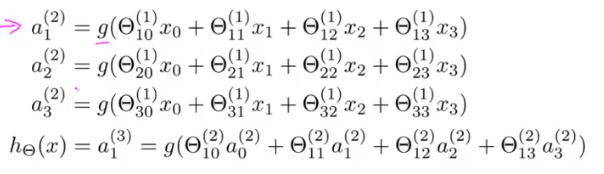
设z=前一层的拟合函数,如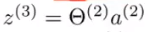
则下一层的拟合函数可表示为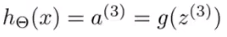
可以用神经网络实现与、或、非、与非等逻辑判别:
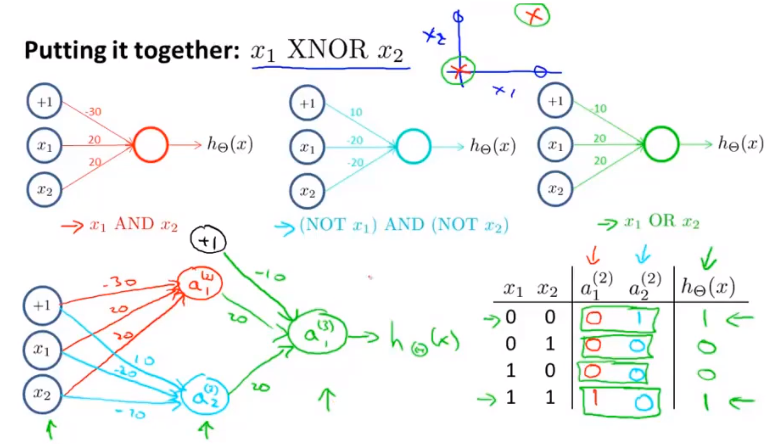
代价函数
逻辑回归代价函数
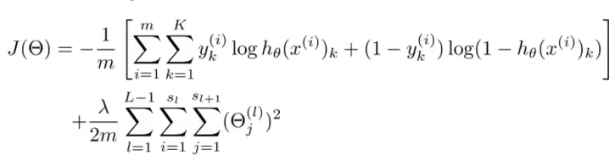
均方误差
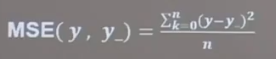
反向传播(BP)算法
从前向后计算误差,从后向前对参数求导
前向传播:
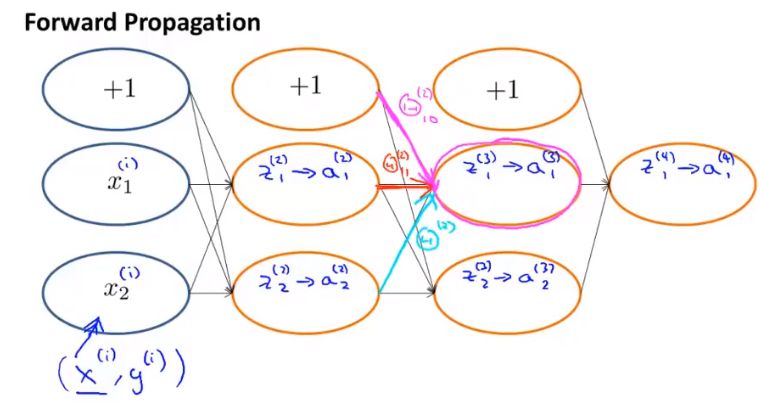
反向传播:
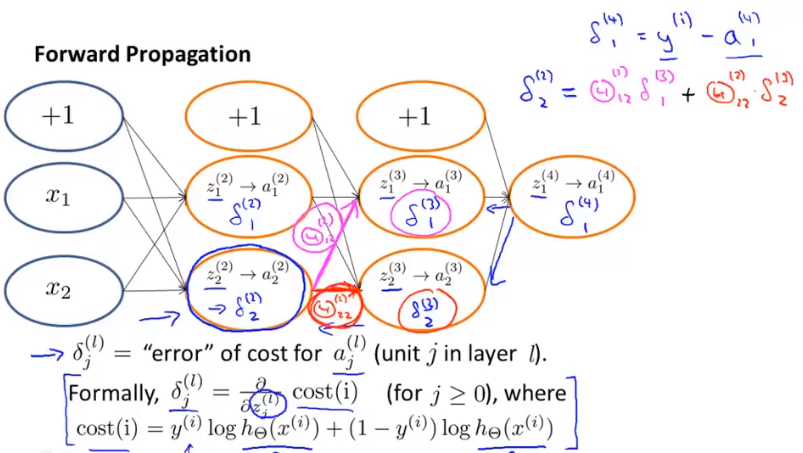
算法参照https://blog.csdn.net/ft_sunshine/article/details/90221691
梯度检测
对每一个θ使用双侧差分来近似获得偏导

缺点:比反向传播慢得多
随机初始化
若一层layer中的每个θ都被设置成同一值(如0),那么每次经过梯度下降更新θ时J(θ)和θ都会取得相同的结果,造成隐藏层的冗余。
随机初始化能够较好的解决这一问题

INIT_EPSILON为[-ε,ε]之间的一个随机值
神经网络实现流程
- 选择网络结构:通常只有一个隐藏层,隐藏层元的数量需要一致
- 随机初始化
- 前向算法计算假设函数h_θ(x)
- 实现算法计算代价函数J(θ)
- 后向算法计算偏导数
- 用梯度检测计算检验后向算法是否正常运行,若正常则取消梯度检测
- 使用梯度下降或其他高级算法减小代价函数
无监督学习
由无标签数据集∑(x_i)进行模型训练
聚类
k-means
簇分配策略
m表示数据数量,K表示聚类中心个数

若出现无点聚类中心,一般会直接移除这个中心,若确实需要K个中心,则可以将这个中心重新随机初始化
代价函数
失真函数

c_i为xi距离最近的簇中心的距离,μi为各个簇心位置

先固定μi计算c_i的代价函数,在计算μi的代价函数
多次随机初始化来防止局部最优解(K较小时比较有效)
K的选择
肘部原则
从1逐渐增大k的个数直到m,对于每一个k值计算失真函数,选择如图的”肘部”作为聚类的个数
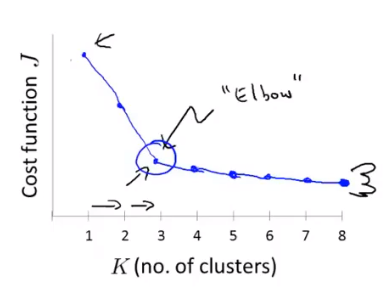
缺点:得到的图像不一定都有”肘部”,难以确定聚类个数
下游目的决定K值:根据聚类的目的决定
降维
二维降一维
将二维特征投影到一维直线上
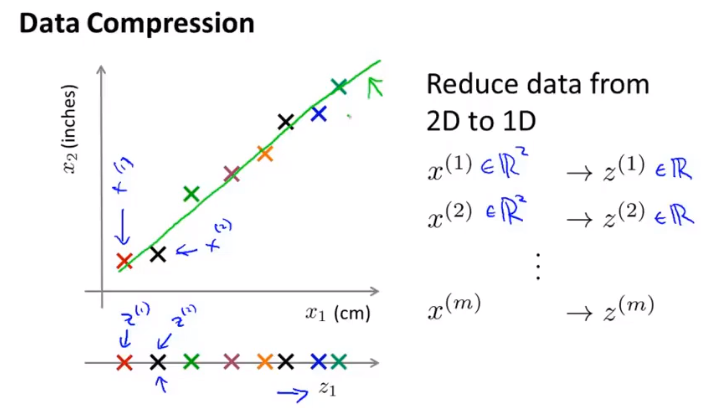
三位降二维
将三位特征投影到二维平面上
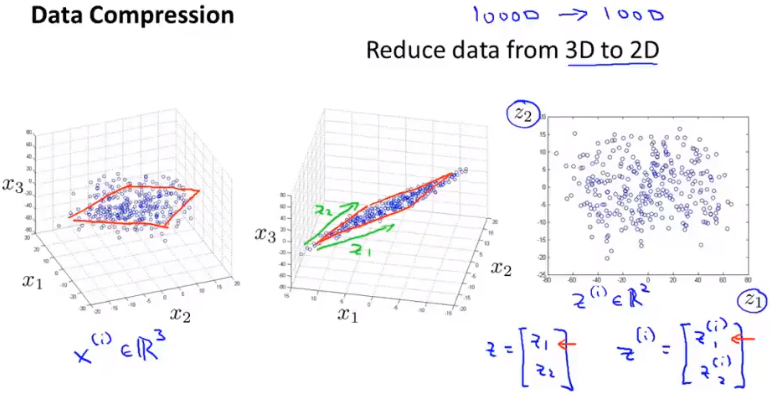
主成分分析(PCA)
将所有特征投影到低维平面,本质:舍弃掉一些信息来降低维度
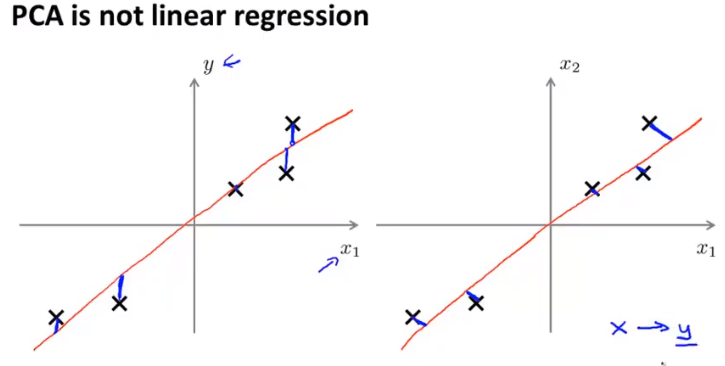
与线性回归差异:线性回归为y与预测值之间的差,而PCA为与该方向距离的差,即每个特征具有同等地位
最近重构性:样本点到该支线距离足够近
最大可分性:样本点在这个直线的投影尽量分散
svg/eig函数输出结果

输出U为n乘n矩阵,选取前k列进行转置后乘x矩阵,得到一个输出n乘k矩阵即为降维结果

选择压缩维度K
选择<=0.01表示保留99%的方差


从K=1开始不断增大K值,直到满足check式,使用svd函数一次返回的s矩阵可以满足K=1到K=n的要求
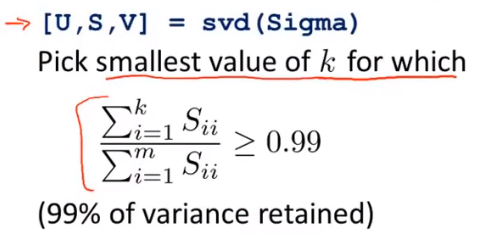
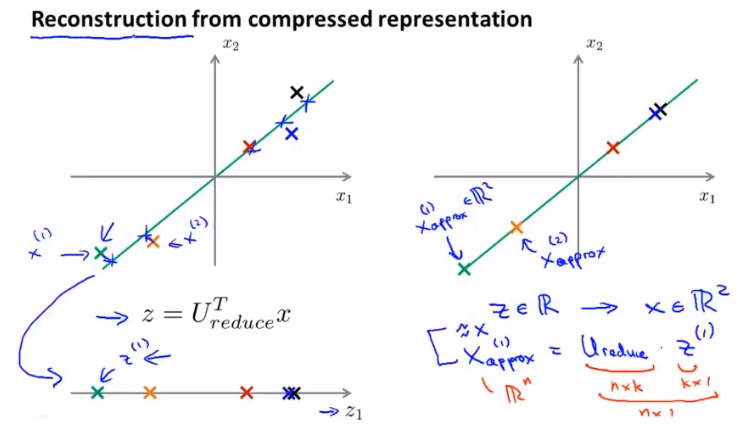
压缩重现
有损失x=Uz
运用PCA
PCA运用在训练集上,当建立了从x到z的映射后再将映射应用在交叉验证集和测试集上

PCA不推荐应用于过拟合问题的处理上,因为PCA不顾y值,仅依靠x值来判断舍弃一些信息
当模型的运行过于缓慢,计算量过大时推荐使用PCA,以减少对内存和硬盘空间的需求,或用来可视化数据(需要较低的维度)
异常检测
当p<设定值ε时判断为异常
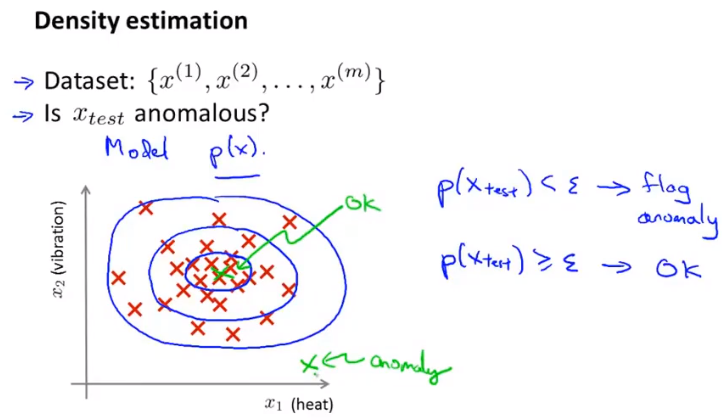
高斯分布(正态分布)
使用独立概率的高斯分布作为p函数

带标签数据
一个数据集中有数个已知异常样本,将这些样本仅放于交叉验证集和测试集中
用训练集来拟合p函数

评估异常检测模型

异常检测vs监督学习

若负样本远多于正样本使用异常检测,若正样本较多则使用监督学习
选择异常检测的特征
对于非高斯特征,调用对数或幂函数使其满足高斯分布的特征
也可以根据实际情况根据已有特征创造出新的特征,如

多元高斯分布
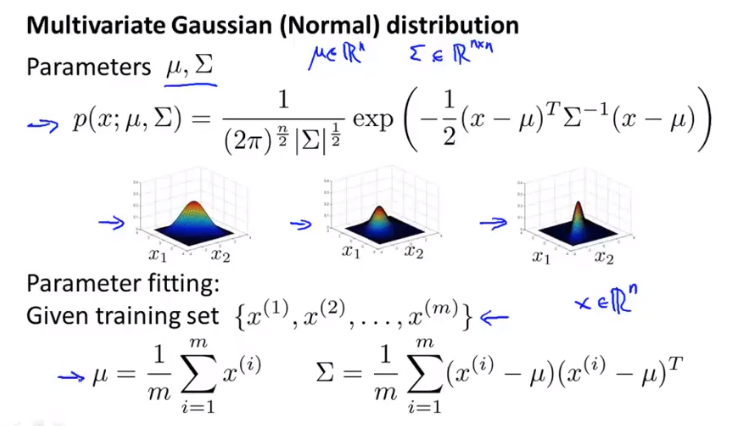
多个单独的高斯分布无法正确的判别异常时,选择P~N(μ,Σ)作为检测函数,其中,μ为n1矩阵,Σ为nn协方差矩阵(Σ元值可设为负值)
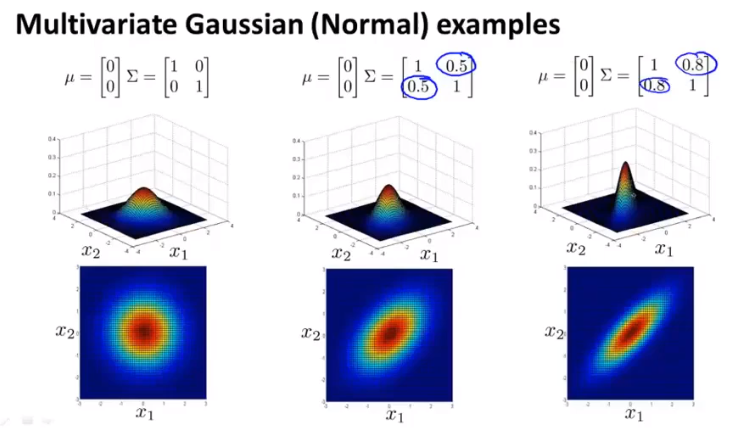
原始模型/多元模型

原始模型需要人工选择特征之间的关系,多元模型能够自动分配关系;由于多元计算的复杂性一般仅当m>>n(m>=10n)时才选择多元高斯分布
推荐系统
案例:电影推荐
将每一部电影的特征分别表示维xi,将每个用户的偏好表示为θ,用户的接受程度就是θTx
根据电影特征估计用户评分x->θ
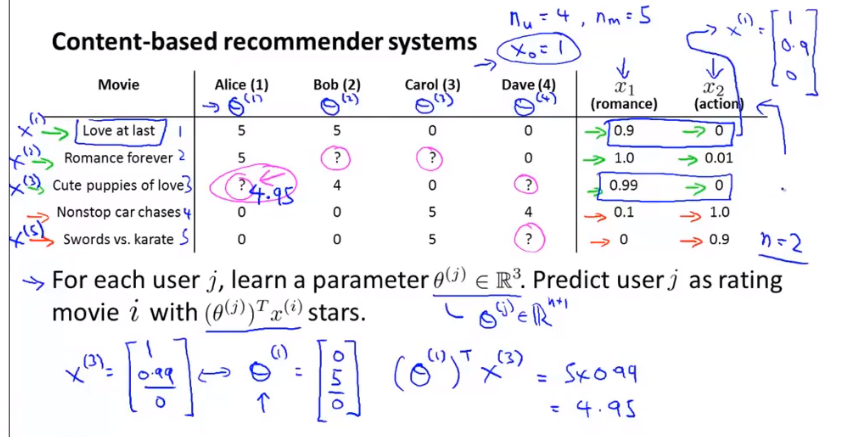

优化函数,1/m不影响函数本身,因此省略

协同过滤
特征过滤
通过用户的评分可以反向判断出电影特征θ->x
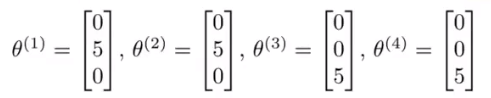
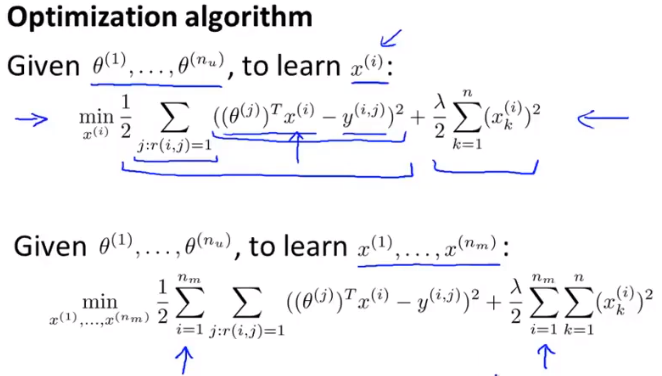
经过不断过滤可以最终收敛到合理的θ和x值
协同过滤算法
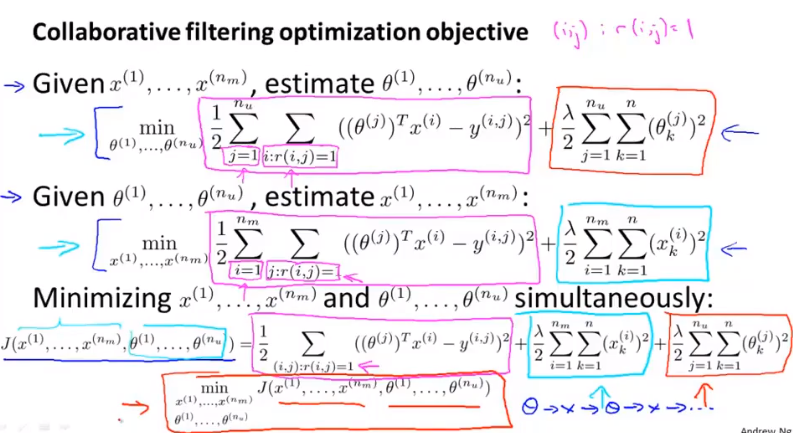
不需要设置x0=1,算法会由其需求自动修改

向量化实现
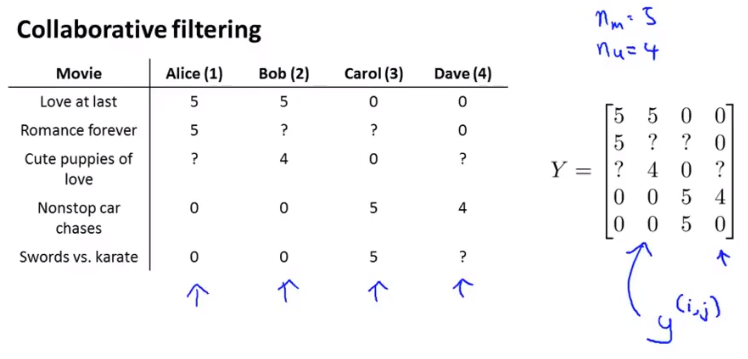
将评分数据转换为矩阵
低秩矩阵分解

推送最相关的内容

均值归一化
添加新用户时,θi=0,θTx恒为0
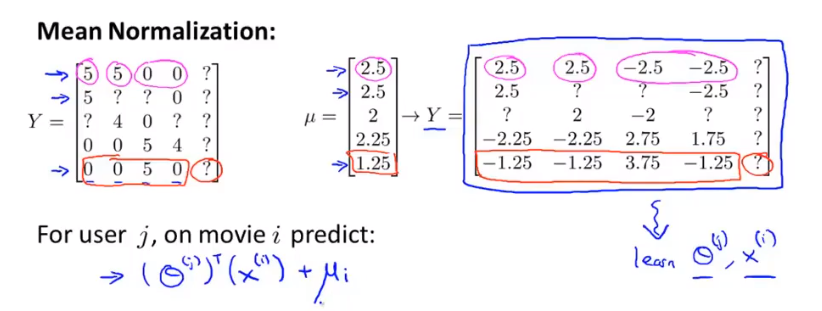
令Y矩阵=X矩阵,Y的每一项减去这一行的均值
大规模机器学习
进行大数据集的学习
随机梯度下降
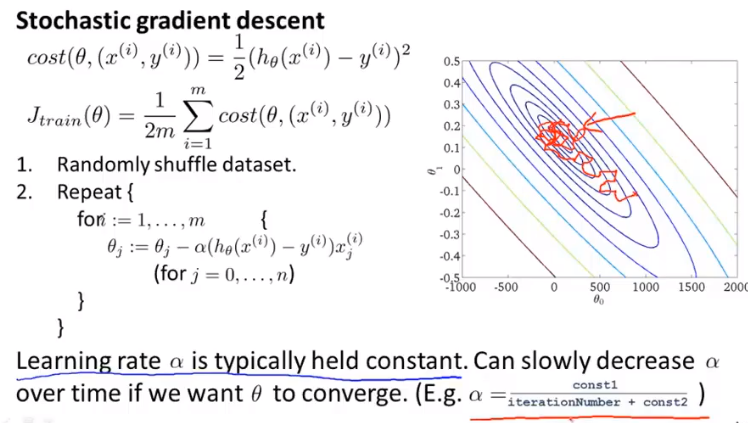
Stochastic梯度下降
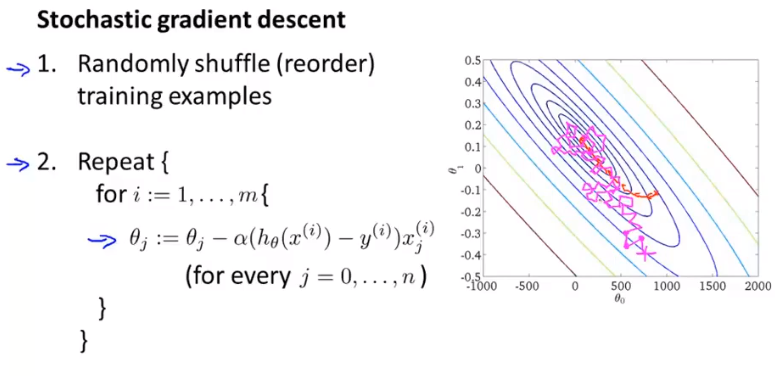
Stochastic梯度下降对于每一个数据xi都进行一次θ的更新,拟合的过程也与批量梯度下降不同,最终会落在全局最小值附近,需要自己选择重复次数来使模型可用
Min-batch梯度下降
使用较小的批量大小,一般在有合适的向量化表示时选择这种算法
1<b<100

检验梯度下降
每隔(如1000)次迭代后画出代价函数的图像,当增大每次间隔的迭代次数时曲线会变得更加平滑,更容易看出总体趋势
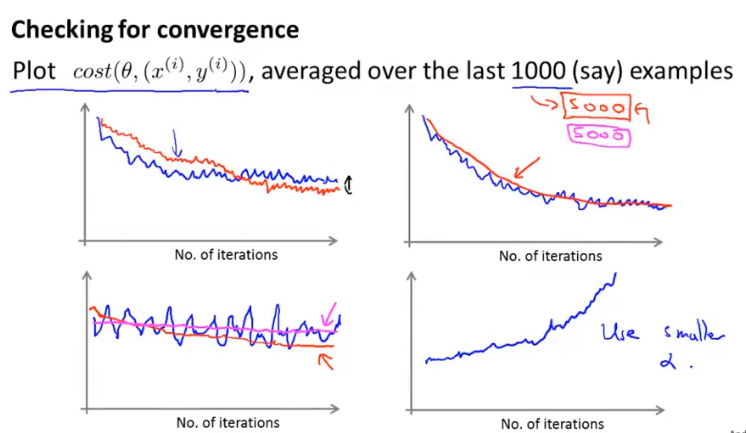
为了让随机梯度下降更好的收敛,可以设置α随迭代次数的增大慢慢减小
动量梯度下降

动量可以理解为每次迭代具有前一次迭代的惯性
在线学习
通过持续不断输入的数据进行学习,类似Stochastic梯度下降,并舍弃已使用的数据
MapReduce

用来处理一台电脑无法处理的大规模数据问题,每个机器计算数据集的一部分,并将结果送至中央服务器结合更新θ
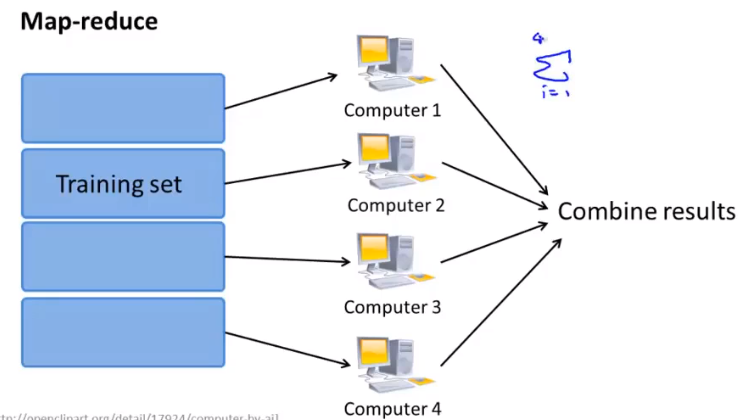
在一个计算机中应用(多核)
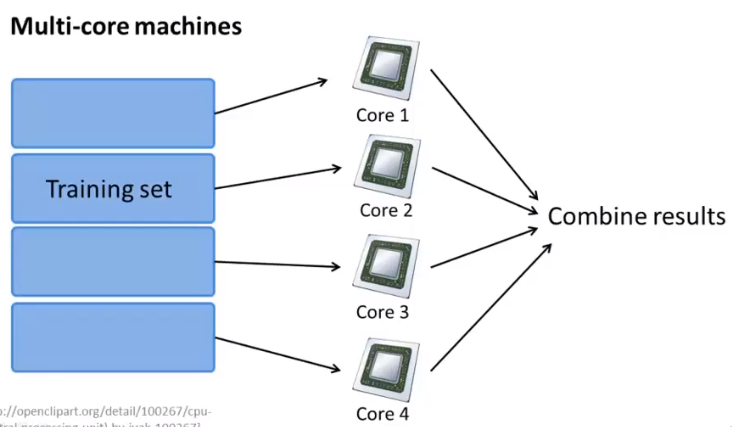
案例分析
OCR图像识别
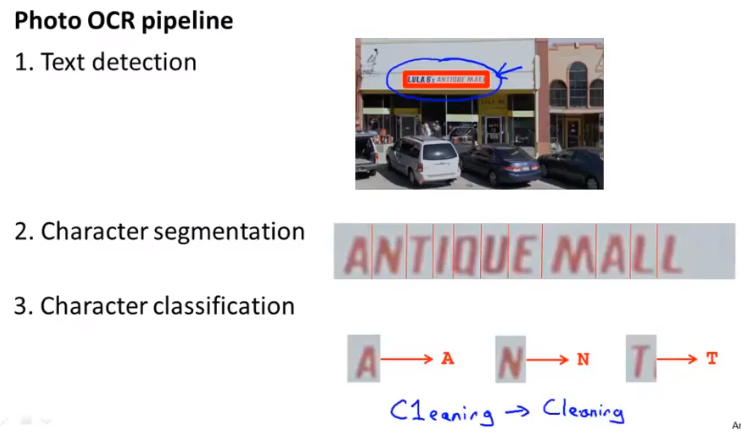
识别出图像中的文字信息
- 定位文字位置区域
- 对文字进行标记和分割
- 进行文字识别
- (识别纠正)
流水线工作流程

行人检测系统
将图像分割成同一大小的正样本和负样本
识别对象

滑动窗口
- 对一个小的图像区域进行检测,然后将图像区域向右移动一个参数值,行末移至下一行进行遍历
- 增大图像区域大小,将截得到的图像进行缩放至原有大小再次遍历,重复这一过程
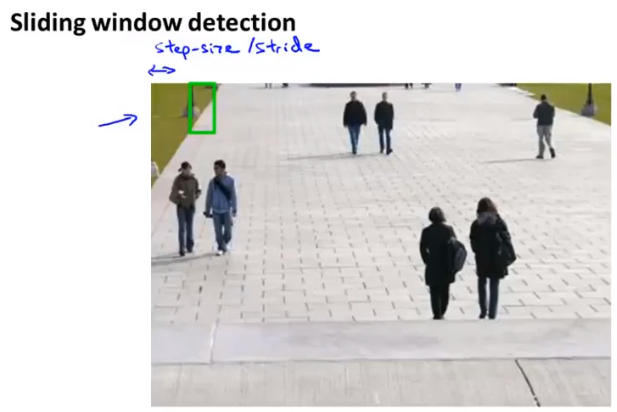
这一识别方法可以同样应用于文字识别的定位步骤
放大算子
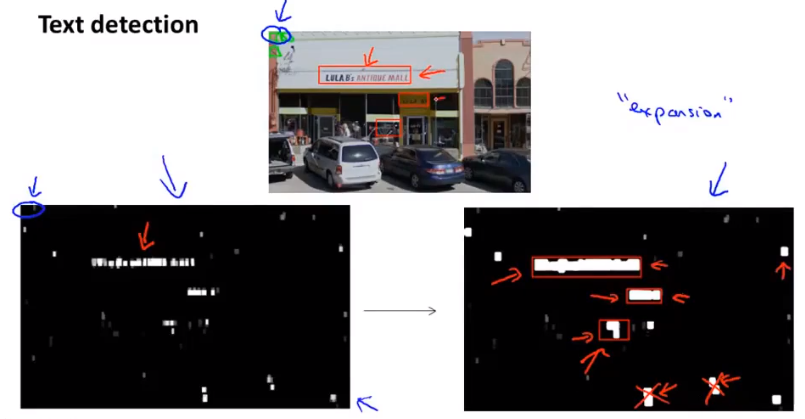
识别识别到的区域周围是否有其他识别到的区域,缩小其间距来进行区域链接,舍弃不合理的区域之后在周围添加矩形边框。
分割字符
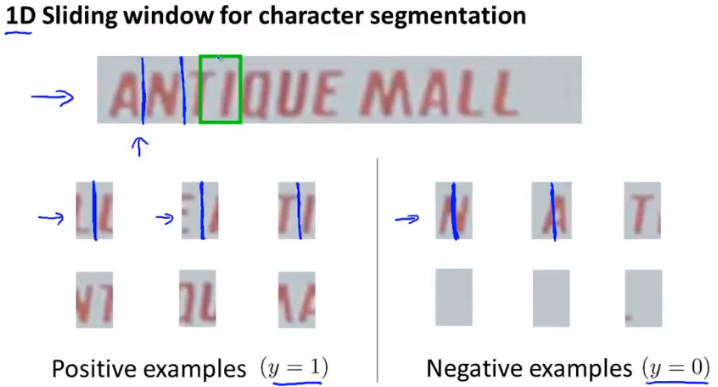
一维:训练模型后从左到右进行识别
人工数据合成
先确定增加训练样本数量能够提升算法效率再进行样本数据的扩充
从零生成新数据,如将一种字体转换成一种新的字体
转换已有数据(失真合成数据),如
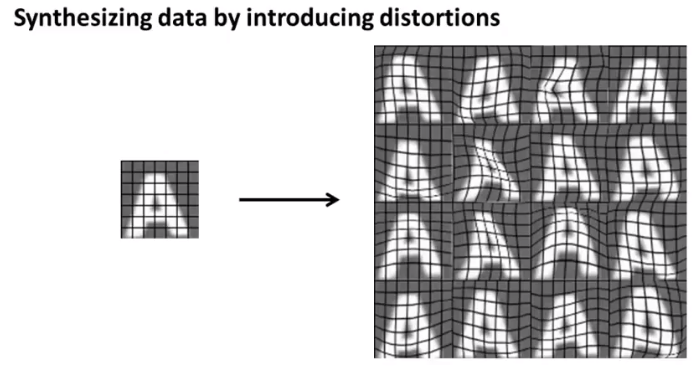
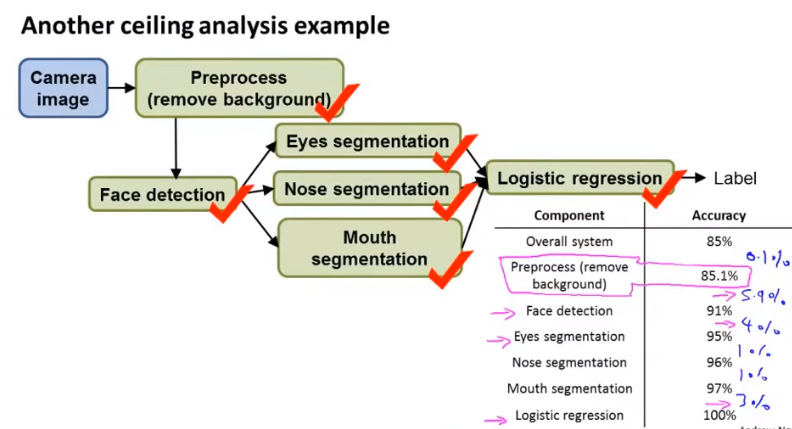
上下限分析
对算法进行优化时预测每一步的优化对于准确率的影响,据此决定优化方向流水线的哪一部分
卷积神经网络
边缘检测示例
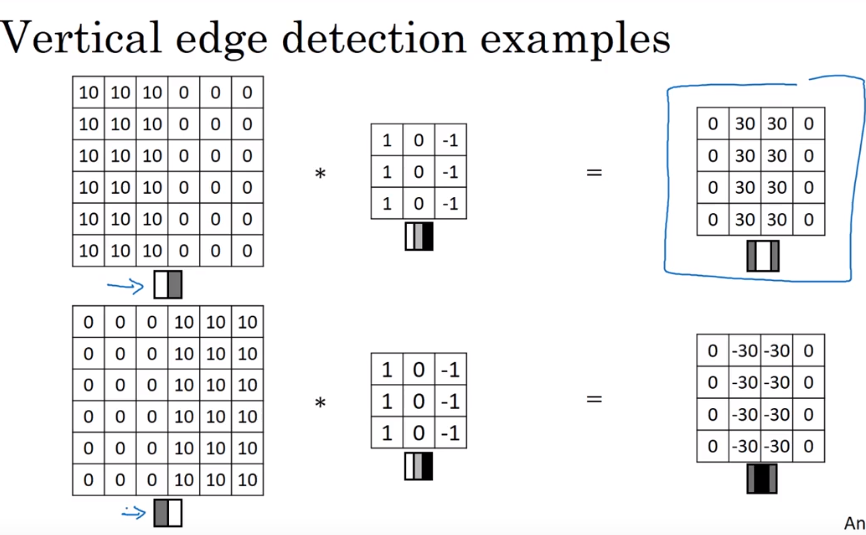
Padding
用0像素点来填充边缘
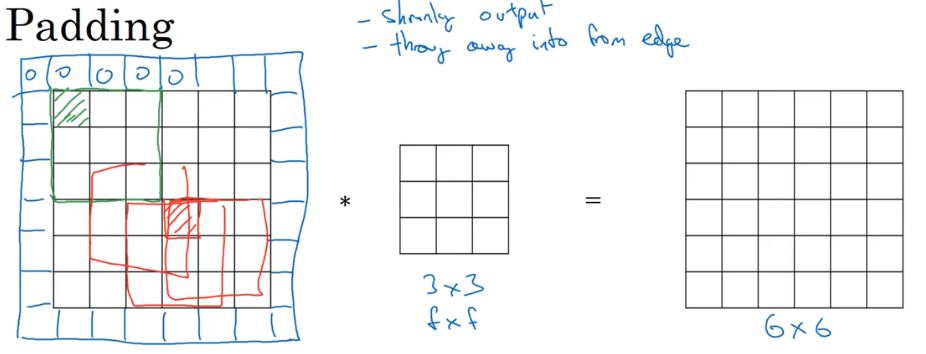
- 不使用Padding时图像会持续缩小,下一层的图像边长为n-f+1;使用Padding填充边缘使得下一层图像边长变为n=2p-f+1,当填充的像素点边长p=(f-1)/2时下一层的图像边长将于上一层相等。(f大多数都是奇数)
- 不使用Padding时图像边缘得像素点信息无法得到有效利用,而使用Padding能够减轻这一后果
Valid卷积:不填充
Same卷积:输出大小等同输出大小
步长Stride
卷积核向右或向下移动的步长s,则输出的图像大小为[(n+2p-f)/s+1],若不为整数则向下取整
三维卷积
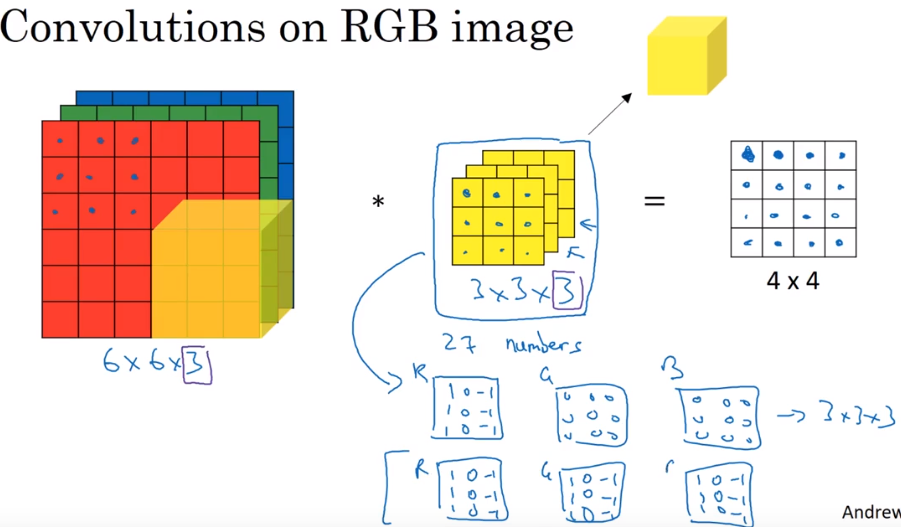
通过设计不同通道得卷积样式来获得不同的输出效果,通道数与输入通道数必须相同
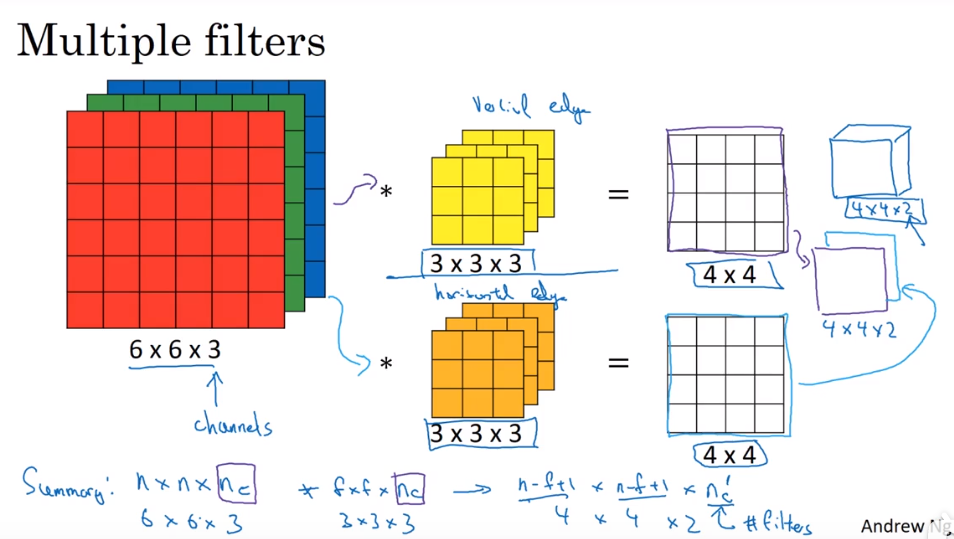
添加多个过滤器来提取不同的特征,然后将各过滤器输出结果作为不同维度合成为一个立体输出层
输出层的维度(通道数)等于过滤器的个数(提取的特征量)
一般来说,随着卷积神经网络层数的增加,输出层边长不断减小,维度不断增大
池化
最大池化/平均池化:在一个过滤层大小的位置上选取最大值或平均值直接输出
池化层没有权重和参数,只有超参数,因此在计算卷积神经网络层数时经常把池化层和卷积层合并算为一层
超参数:
- f:卷积核大小
- s:步长
卷积神经网络示例