Lzone

always be doing

0%

机器学习流程

发表于 更新于 分类于
本文字数： 3.3k 阅读时长 ≈ 3 分钟

机器学习流程

深度学习笔记参考

https://blog.csdn.net/zouxy09/article/details/8775360

四种基本神经网络参考

https://blog.csdn.net/kwame211/article/details/110382931

基础概念

注：未特殊声明时*表示必填

数据集：特征值+目标值

按目标值分类

监督学习

有目标值类型

1
2
类别						  分类问题
连续型数据					回归问题

分类：k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、SVM

​ 回归：线性回归、岭回归

生成模型

学习总体情况

img
判别模型

学习类别之间的差异

没有目标值

聚类：k-means，高斯混合模型

其他学习

  • 半监督学习：给少量数据和大量未标注数据
  • 增强学习：对于输出结果只给出评价信息而不给出正确答案
  • 多任务信息：多个相关任务一起学习

机器学习开发流程

获取数据->数据处理->特征工程->机器学习算法训练模型->模型评估->应用

数据处理

数据清洗

完整性、合法性、一致性、唯一性、权威性

数据采样

避免数据不平衡，比如正类与负类样本数量差距过大

解决方法：

  • 过采样：随机复制少数类样本数量
  • 欠采样：随机消除多数类样本数量

数据集拆分

训练数据集：构建学习模型

验证数据集：辅助或在构建过程中评估，用于调整参数

测试数据集：最终评估

拆分方法：

  • 留出法：直接对数据集进行划分，如70%/30%

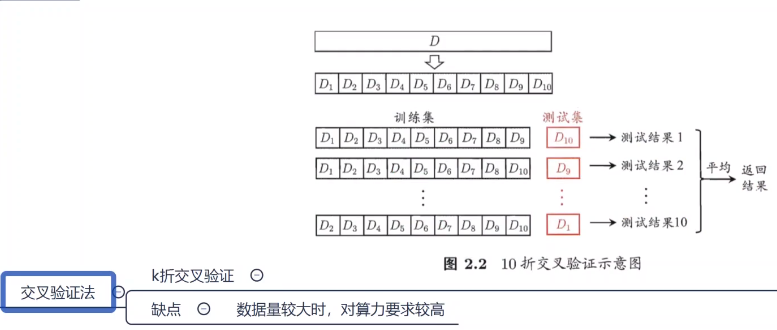
  • k-折交叉验证法：将数据集划分为k个大小相似的互斥子集，进行k组训练和测试，k常取10

    image-20210123204645757

特征工程

特征选择

过滤法，包裹法，嵌入法

特征降维

主成分分析（PCA）

线性判别分析（LDA）

特征编码

one-hot

语义编码

规范化

机器学习方法

分类问题

决策树

由不同的特征值构建分支

过程：从根节点开始测试待分类项中相应的特征属性，并按照输入值输出分支，直到叶子节点作为决策结果

img

决策树特征选择

  • 信息熵

    image-20210125203603626

    不等概率的信息熵

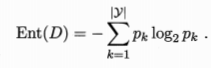
    image-20210125211402128

  • 信息增益=信息熵（前）-信息熵（后）

  • 信息增益比=惩罚参数*信息增益；特征个数越多惩罚参数越小

  • 信息增益率

    img

    其中Gain(D,a)为该分支的信息熵数值

  • 基尼系数：表示集合不确定性，越大表示不平等程度越高；一个属性的基尼指数为该属性所有分支的加权和

    image-20210126132100247

决策树构建算法

img

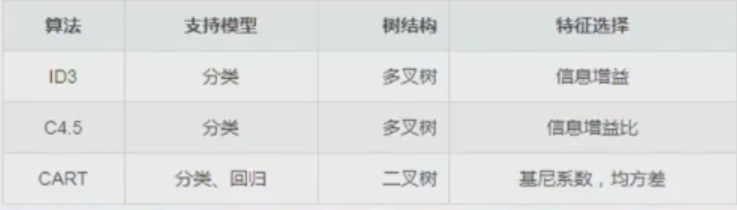
ID3算法

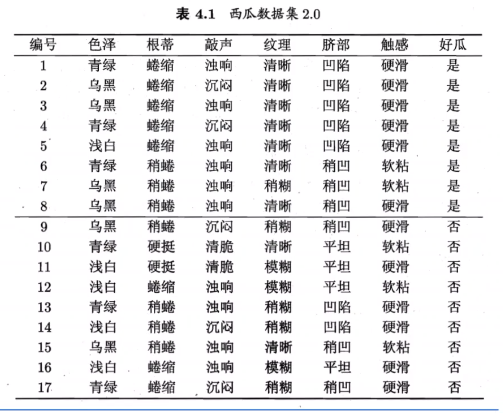
image-20210125214254688

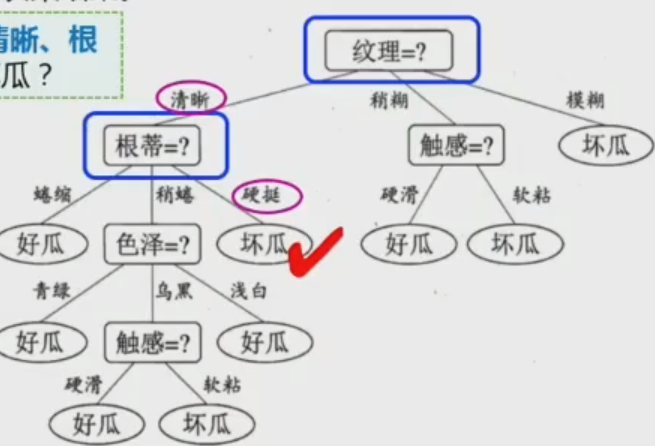
在所有信息中选择获得该信息之后信息增益最大的信息作为根节点(如纹理信息获得信息增益最大，为0.381bits)，之后同理。

C4.5算法

对于连续值得处理，将一个属性的数值从小到大排序，分别取不同的阈值进行分类，计算信息增益，选取信息增益最大得阈值作为所取阈值。

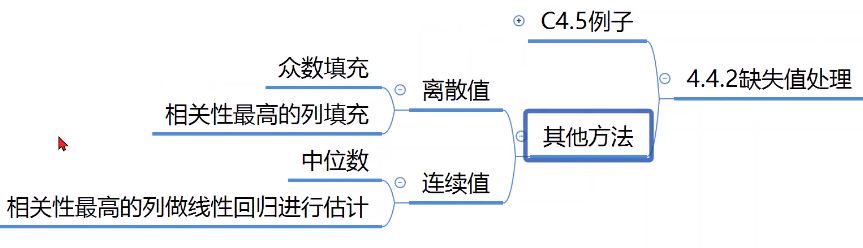
缺失值处理

image-20210127142939815

CART算法

计算每个属性的基尼指数，在所有属性中选择基尼指数最小的作为根节点，以此类推，当子节点的基尼指数不再降低(不变或升高)时中止分叉

决策树剪枝

理想的决策树：叶子节点最少，叶子节点深度最小，或两者的结合

修正方法：

  • 预剪枝(自上而下)

    image-20210126135721935

    当一个属性分支之后正确分类的样本数比之前少时取消该分支

    • 预先设置高度，当决策树到达该高度时停止生长
    • 到达某节点实例具有相同的特征向量
    • 定义一个阈值（实例个数、系统性能增益等）

  • 后剪枝(自下而上)

    与预剪枝相反，从最底层叶子节点开始，判断剪枝之后正确分类的样本数是否比之前少，正确数减小则不剪

    先构建决策树，对置信度不够的结点字数用叶子节点代替，该叶子节点类标号用该结点子树中最频繁的类标记。这种方法相比于预剪枝更为常用

贝叶斯分类

优点：算法逻辑简单、易于实现；分类过程时空开销小

缺点：贝叶斯模型假设各属性之间互相独立，实际应用中往往不成立，属性个数多或相关性大时效果不好

贝叶斯公式

  1. 计算先验概率
  2. 为每个属性计算条件概率
  3. 计算后验概率

使用极大似然法计算概率

朴素贝叶斯分类器

分别计算处于当前属性各分类得概率判断属于某一分类

避免”一票否决“：拉普拉斯修正

EM算法

image-20210127172318696

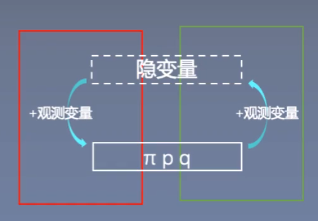
image-20210127171514425

？SVM（支持向量机）

SVM

对一些数据点进行分类，当超平面离数据点间隔越大，分离的确信度也越高

SVM寻找一个最优决策边界，使距离两个类别最近的样本最远

  • 硬间隔支持向量机
  • 软间隔支持向量机（对异常点支持
  • 非线性支持向量机与核函数

优点：不需要过多样本；结构风险最小；非线性

方法

  • Maximal margin classifier

    image-20210127144707782

    直接选取最大值最小值之间平均作为阈值

  • Support Vector Classifier
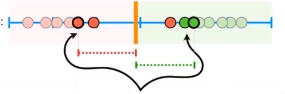
    image-20210127144836998

    中间作为缓冲区域，中间的向量称为支持向量(support vector)

  • 使用核函数升维或降维

使用拉格朗日乘数法求极值

多分类SVM

  • 一对多法：把某个样本分为一类，剩余所有样本分为一类，k个样本构建出k个SVM

    分类时将未知样本分类为具有最大分类函数值的一类

  • 一对一法：任意两个样本之间设计一个SVM，k个样本共设计k(k-1)/2个SVM

    分类时将位置样本分类为最后得票数最多的一类

  • 层次支持向量机：将所有类别分成两个子类，再将子类进一步划分为两个次级子类，直到得到一个单独的类别

？逻辑回归

二项逻辑回归

img

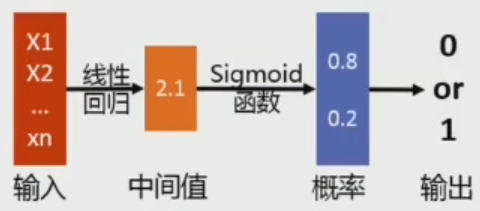
多项逻辑回归

学习多个w参数

集成学习

将多个弱分类器集成在一起共同完成学习任务（严格来说不是一种机器学习算法，而是一种优化策略）

Bagging(bootstrap aggregating)

基于数据随机重抽样得分类器构建方法，统计多个模型对同一数据集的输出结果，输出投票最高者为最终结果

Boosting

集中关注被已有分类器分类错误的样本，构建新的分类器，输出结果正确率高的模型得到权重更高

优点：比单个模型预测的结果精确的多，被普遍使用

缺点：需要大量维护

回归问题

线性回归

一般流程：

  1. 选择拟合函数形式
  2. 确定损失函数性质
  3. 训练算法如最小二乘、梯度下降等方法找到回归系数
  4. 使用算法进行数据预测

线性回归扩展

多项式拟合

？过拟合

所得回归表达式可以较为完美的描述训练集上的每一个点，但跟实际需要的模型相差很大

方法：

  • 岭回归：规定参数β和λ约束方程

    岭回归为二次约束

  • Lasso回顾（套索回归）：

    Lasso回归为一次约束

聚类问题

K-means

属于硬聚类，一个点只能属于一个类别

img

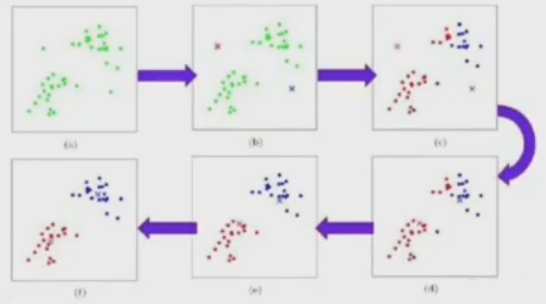
优点：原理简单，实现容易，收敛速度快；聚类效果较优；只需调整参数k

缺点：k值不好把握；不平衡数据集效果不佳；迭代方法结果局部最优；对异常点较敏感

高斯混合模型

EM算法

算法与k-means相似，属于软聚类，一个点可以有多个概率分别属于不同的分布

密度聚类算法

img

以距离任意点一定长度之内的点集作为分类标准

缺点：有一些点因为规模不够而无法构成一个类，同时因为距离不够无法被归入其他类

层次聚类

img

其他问题

隐马尔可夫模型

隐马尔可夫模型两个假设：

隐马尔可夫模型三个基本问题：

应用：词性标注、中文分词、天气预测等

LDA模型

文档生成器

机器学习模型评估

性能评价指标-分类

  • 准确率：分类中正确记录个数占记录总数的比
  • 召回率（查全率）：分类样本正例多少被预测正确了
  • AUC曲线
  • PR曲线
  • 宏平均（全局）/微平均（细微）
  • 对数损失

通常准确率越高召回率越低

性能评价指标-回归

  • 平均绝对误差
  • 平均平方误差
  • R Squared

性能评价指标-聚类

  • 外部指标

  • 内部指标

模型选择优化

  • 泛化误差：在“未来样本”上的误差
  • 经验误差：在训练集上的误差

优化方法：

  • AIC准则：对训练模型加以复杂度的约束
  • BIC准则：增加训练集复杂度

图像识别技术

步骤：

  • 特征提取
  • 索引技术
  • 相关反馈
  • 重排序

补充方法

特征选择与稀疏学习

信息增益越大，特征越重要

  • 过滤式特征选择

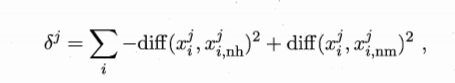
    image-20210127202611593

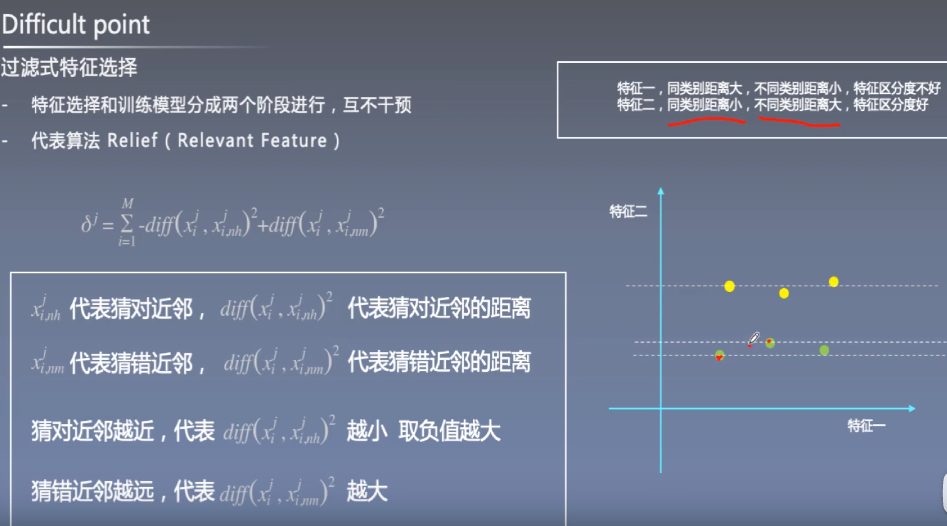
    image-20210127202738083

    该参数越大表示特征越重要，越小表示特征越不重要

  • L1正则化

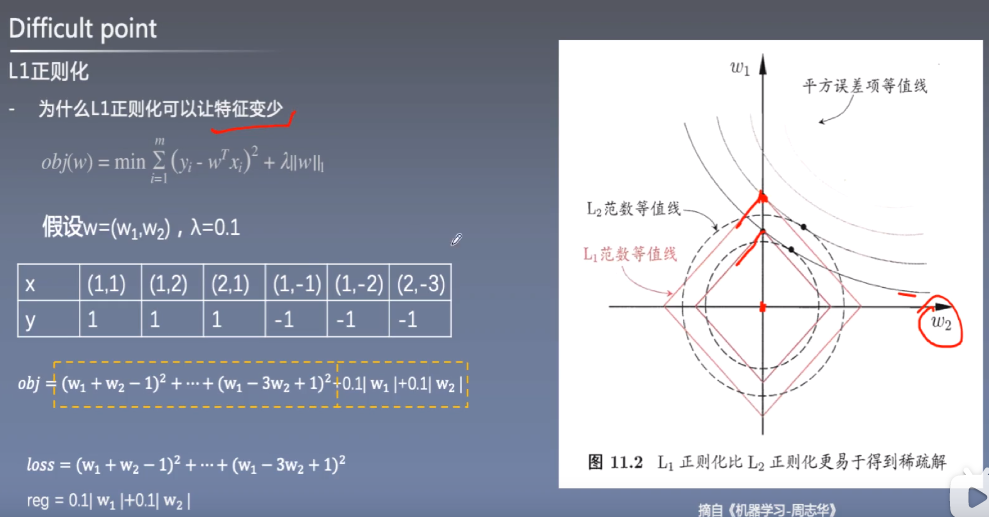
    image-20210127204240828

  • 特征工程

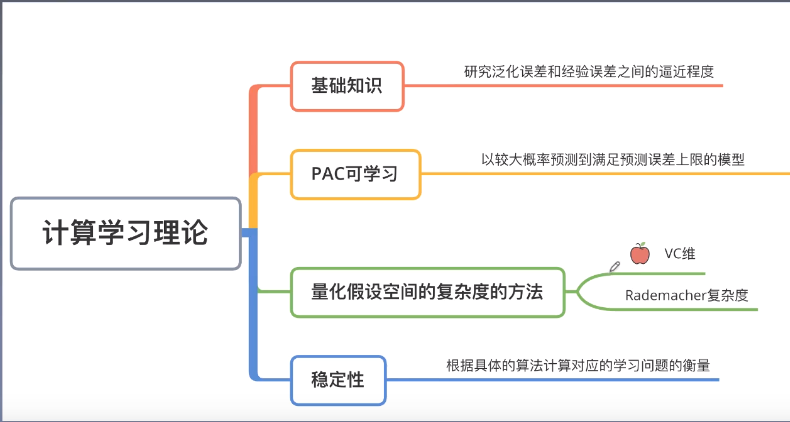
机器学习理论

image-20210127211804309

image-20210127212409103

PAC可学习

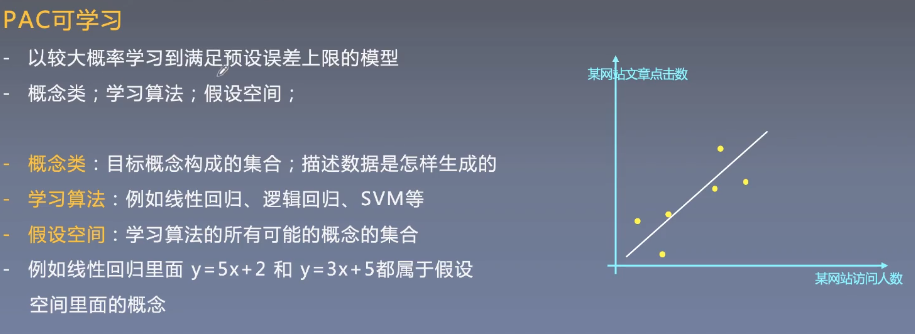
image-20210127212722304

image-20210127212822437

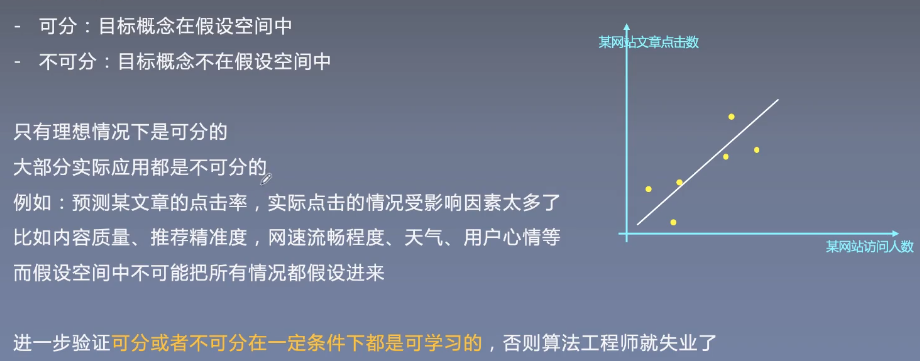
image-20210127213055514

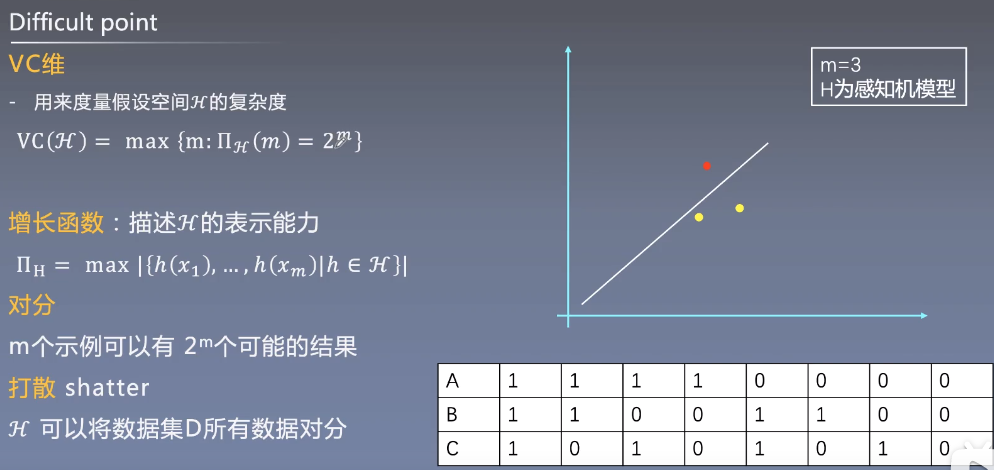
image-20210127213538209

image-20210127213559899

VC维越高，其特征保留能力越强

半监督学习

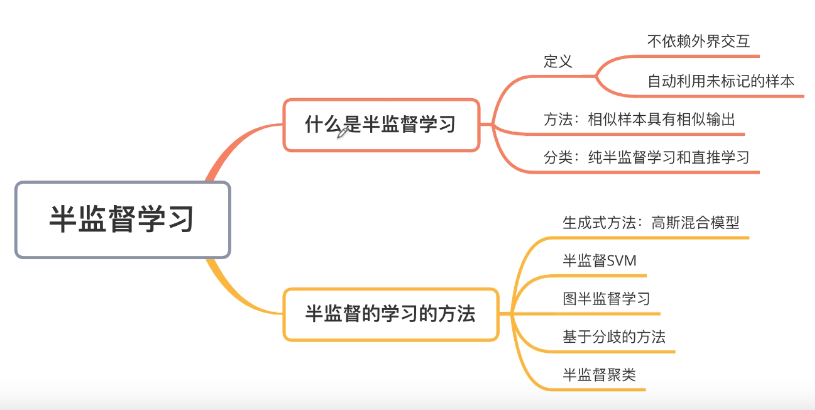
image-20210127214139342

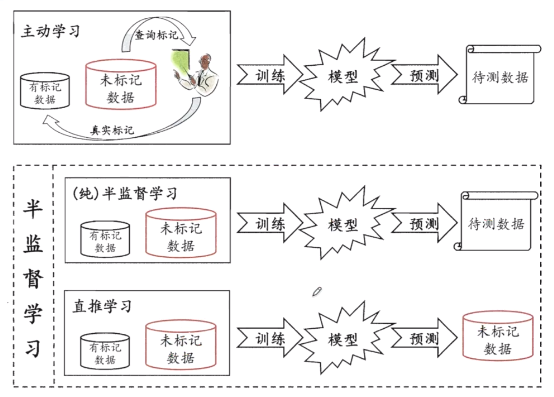
image-20210128144247051

高斯混合模型

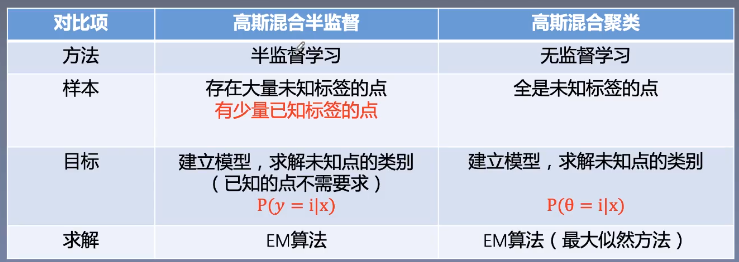
image-20210128144522496

image-20210128144902506

半监督SVM

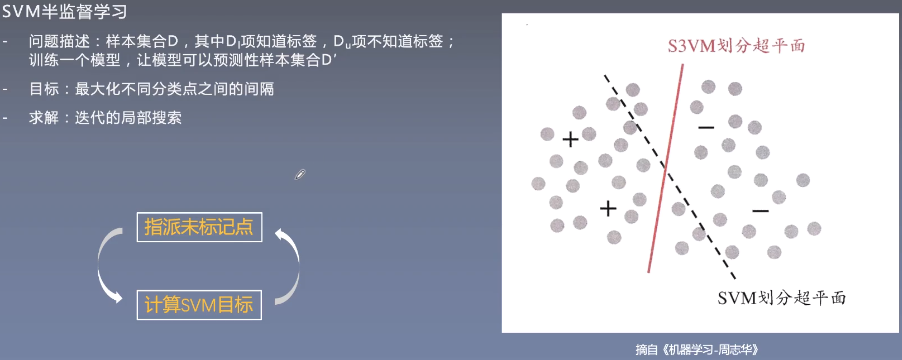
image-20210128145040316

应用：NER等

概率图

概率图模型：用图来表达变量关系的模型

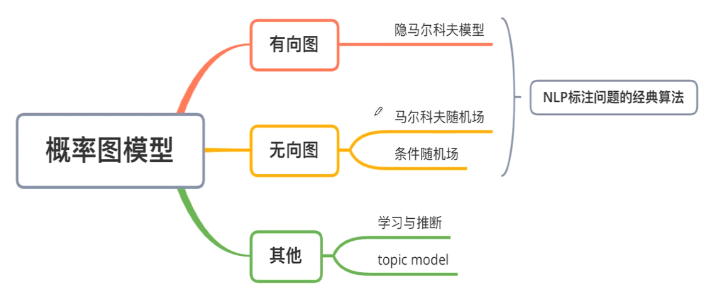
image-20210128145808089

马尔科夫假设

image-20210128145735976

隐马尔科夫模型

image-20210128150002611

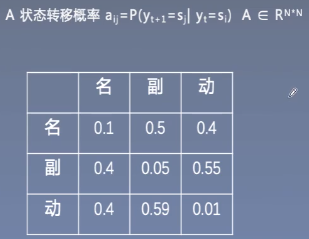
image-20210128150041948

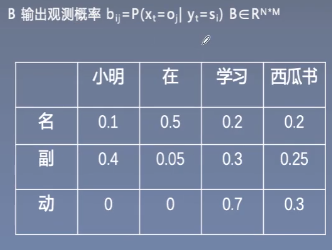
image-20210128150338737

  • π初始状态概率：yi=si得概率
  • A状态转移概率：yi为si，yi+1为sj得概率，即从si变为sj得概率
  • B输出观测概率：观察到的yi状态

image-20210128151426878

用最大似然估计法(或EM算法)来计算各词性得概率，取P最大得此行组合作为预测结果

隐马尔科夫模型模型复杂度

image-20210128161630134

可用维特比算法减少复杂度，即及时除去不需要的路径

规则学习

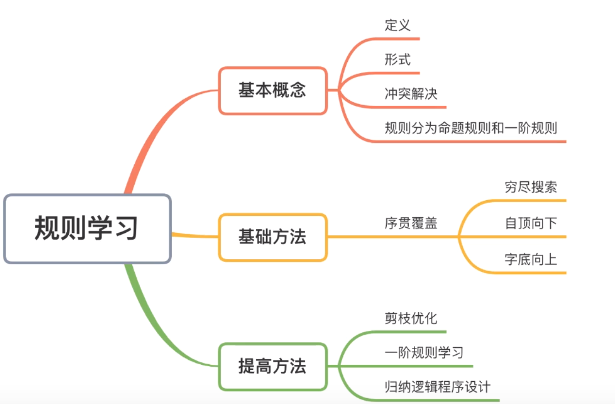
image-20210128161745567

image-20210128161854776

image-20210128162757984

  • 自顶向下–生成测试方法
  • 自底向上–数据驱动方法

强化学习

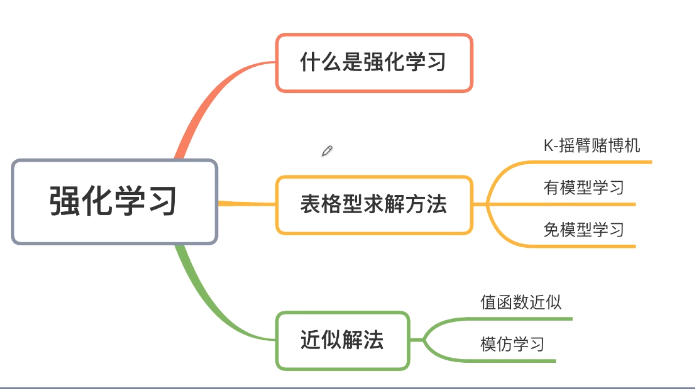
image-20210128200559290

动态分割得思想进行算法分配

image-20210128205715359

当算法效果稳定程度不同时选择不同的算法分配组合

image-20210128205819388

单状态/多状态

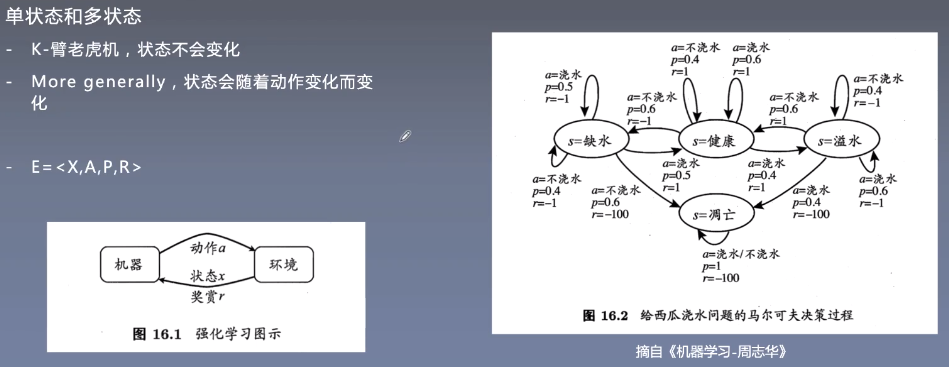
image-20210128205901915

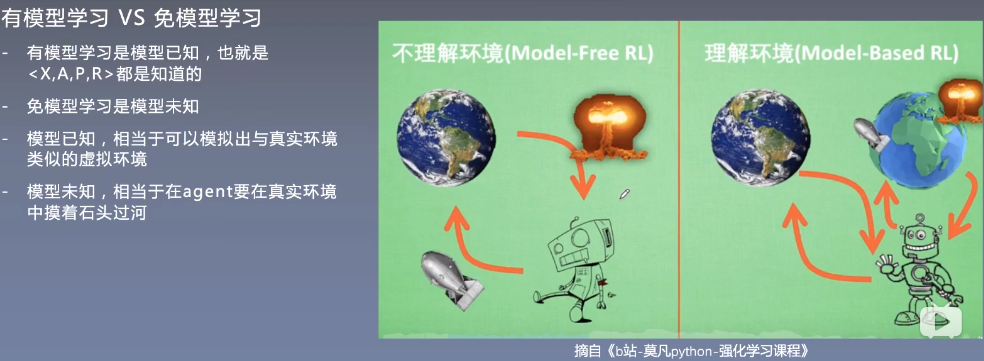
有模型学习/无模型学习

image-20210128210010250