二叉查找树
二叉查找树又名二叉搜索树(BST),与一般的二叉树最大的区别是:任何节点的键值一定大于其左子树中的每一个节点的键值,并小于其右子树的每一个节点的键值。
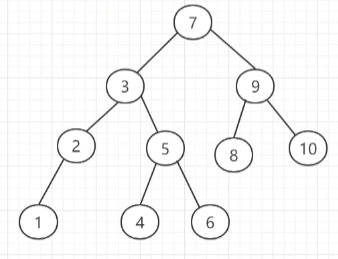
这种树最大的缺点就是极端情况数据结构退化到与链表相似,查找效率低下
AVL树
二叉查找树最大的问题就是如果不手动进行平衡就有可能很快失衡,查找性能下降到与链表相近
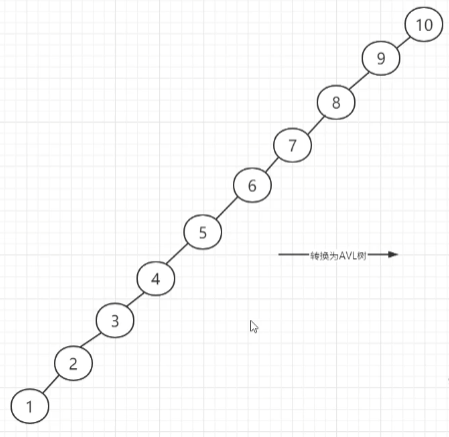
AVL树也称平衡二叉查找树,在插入和删除时会自动根据每个节点的左右结点数进行适当的左旋或右旋
9结点不平衡,右旋:
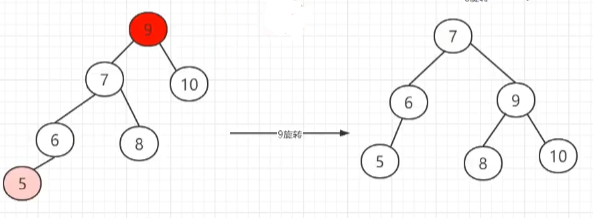
优点:
平衡度很高,查找性能好
缺点:
插入和删除结点时操作繁琐,需要经常进行左旋或右旋操作
B树
B树(B-tree)即多路查找树上面的AVL树也是一种特殊的B树,查找效率为logn
设计成多路是为了降低树的高度,但如果不限制路数的话,结构就会退化成有序数组了。
注意:B树没有要求一定是二叉树,B树的每一个结点都有可能有多于2个子结点
一般会将B树与B+树放在一起比较
B+树
- 有m个子树的中间节点包含有m个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引;
- 所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接,所有叶子结点之间维护了一条链表。 (而B 树的叶子节点并没有包括全部需要查找的信息);
- 所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字,查找效率较为稳定,并且可以很大程度避免随机IO的问题。 (而B 树的非终节点也包含需要查找的有效信息);
2-3-4树
- 2结点:包含1个元素的结点,有2个子结点
- 3结点:包含2个元素的结点,有3个子结点
- 4结点:包含3个元素的结点,有4个子结点
同时满足二叉搜索树的相关特性
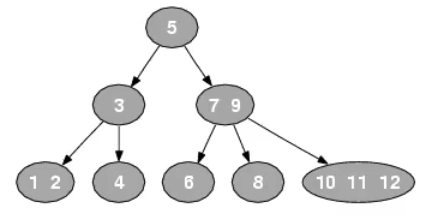
当进行插入时,会尝试合并当前结点,如果当前结点的元素个数等于3,不能继续合并,则中间结点上升,需要插入的结点再向下尝试合并插入
红黑树
也称RBT(Red Black Tree),红黑树是为了简化AVL树的平衡操作而设计出来的,维护效率更高
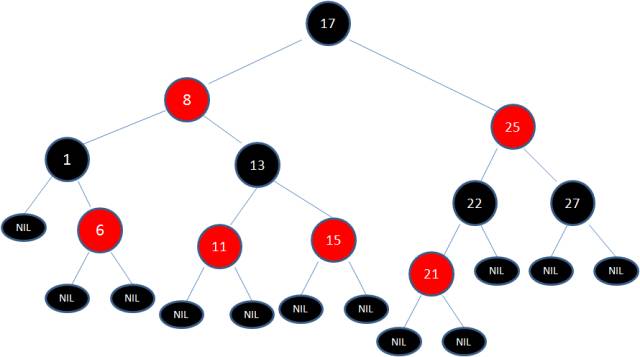
红黑树要求:
- 每个节点要么是黑色要么是红色
- 根节点是黑色
- 每个叶子结点(NIL)是黑色
- 每个红色结点的子结点一定是黑色
- 任意一个结点到每个叶子结点(NIL)的路径都包括数量相同的黑结点
根据上面这些定义,我们可以先一步假设:红黑树与平衡二叉树相比只注重黑结点的平衡,因而效率较高
由于定义5的存在,如果我们新插入结点时插入的是黑色结点,那么一定会打破之前已经平衡了的红黑树的平衡,因此推导出:新插入的结点必须以红结点进行尝试
旋转和变色的情况考虑
一个红黑树结点模拟网站
Red/Black Tree Visualization (usfca.edu)
需要变动的情况:
- 父节点为红:如果父节点为黑,这时插入红色的子结点不会影响红黑树的平衡
- 叔叔结点不存在或叔叔结点为黑色,不论是哪一种情况,必然会使得定义5不平衡
变动的四种具体情景:
- LL型:父节点变黑,祖父节点变红,祖父节点右旋
- LR型:父节点左旋,变为LL型,然后执行LL型的操作
- RR型:父节点变黑,祖父节点变红,祖父节点左旋
- RL型:父节点右旋,变为RR型,然后执行RR型的操作
红黑树与AVL树的比较:
- AVL更平衡,结构上更加直观,时间效能针对读取而言更高;维护稍慢,空间开销较大。
- 红黑树,读取略逊于AVL,维护强于AVL,空间开销与AVL类似,内容极多时略优于AVL,维护优于AVL。
- 基本上主要的几种平衡树看来,红黑树有着良好的稳定性和完整的功能,性能表现也很不错,综合实力强,在诸如STL的场景中需要稳定表现。
- 红黑树的查询性能略微逊色于AVL树,因为其比AVL树会稍微不平衡最多一层,也就是说红黑树的查询性能只比相同内容的AVL树最多多一次比较,但是,红黑树在插入和删除上优于AVL树,AVL树每次插入删除会进行大量的平衡度计算,而红黑树为了维持红黑性质所做的红黑变换和旋转的开销,相较于AVL树为了维持平衡的开销要小得多
综上,如果是查找远多于插入和删除的情境下可以选择AVL树;如果查找、插入和删除的发生频率近似,处于一种综合场景,选择红黑树会是更优的答案